How to Identify a Scalene Triangle

A scalene triangle is a type of triangle where all three sides have different lengths, and all three angles are of different measures. This unique property sets to identify a scalene triangle from other types of triangles, like equilateral triangles, where all sides and angles are equal, and isosceles triangles, where at least two sides (and their opposite angles) are equal.

This article will guide you through how to apart a scalene triangle from all other triangles with easy-to-follow instructions.

Here are some ways to identify a scalene triangle:

1. Check the Side Lengths: In a scalene triangle, no two sides are the same length. Every side is different, so if you measure all three sides of the triangle and they all have different measurements, then you have a scalene triangle.
2. Examine the Angles Measurements: A scalene triangle has no equal angles. If you measure all three angles and find that each angle is different, it confirms that the triangle is scalene.
3. Check for symmetry: Scalene triangles have no lines of symmetry or point symmetry. If you do not find any symmetrical line, then the triangle is surely identified as a scalene triangle.
4. Use a Protractor or Measuring Tool: If you’re working with a physical triangle, you can use a protractor to measure the angles and a ruler to measure the sides. If the measurements for both the sides and angles do not match with each other (i.e., no sides or angles are the same), then the triangle is scalene.
5. Mathematical Approach: One can easily identify a scalene triangle by applying mathematical approach. If you know the lengths of the sides, you can also apply the triangle inequality theorem and verify that the sum of the lengths of any two sides is always greater than the third side. This basic rule applies to all triangles, but it can help you confirm that a given triangle with unequal sides is indeed spotted as a scalene triangle.
6. Visual Identification: Visually, a scalene triangle may look irregular and lack any symmetry. Since all sides and angles are different, it won’t have any equal sides or angles to create a balanced or symmetrical shape.
7. Look for a Lopsided Appearance: Scalene triangles are often easy to spot because they look a little wonky and lopsided. Scalene triangles are not symmetrical, so they have a lopsided look.

Identification of Types of Scalene Triangles

There are three types of scalene triangles:

1. Acute scalene triangles: Have three interior angles measuring less than 90°.
2. Obtuse scalene triangles: Have one angle measuring between 90 and 180°.
3. Right scalene triangles: Have one right angle or 90°.

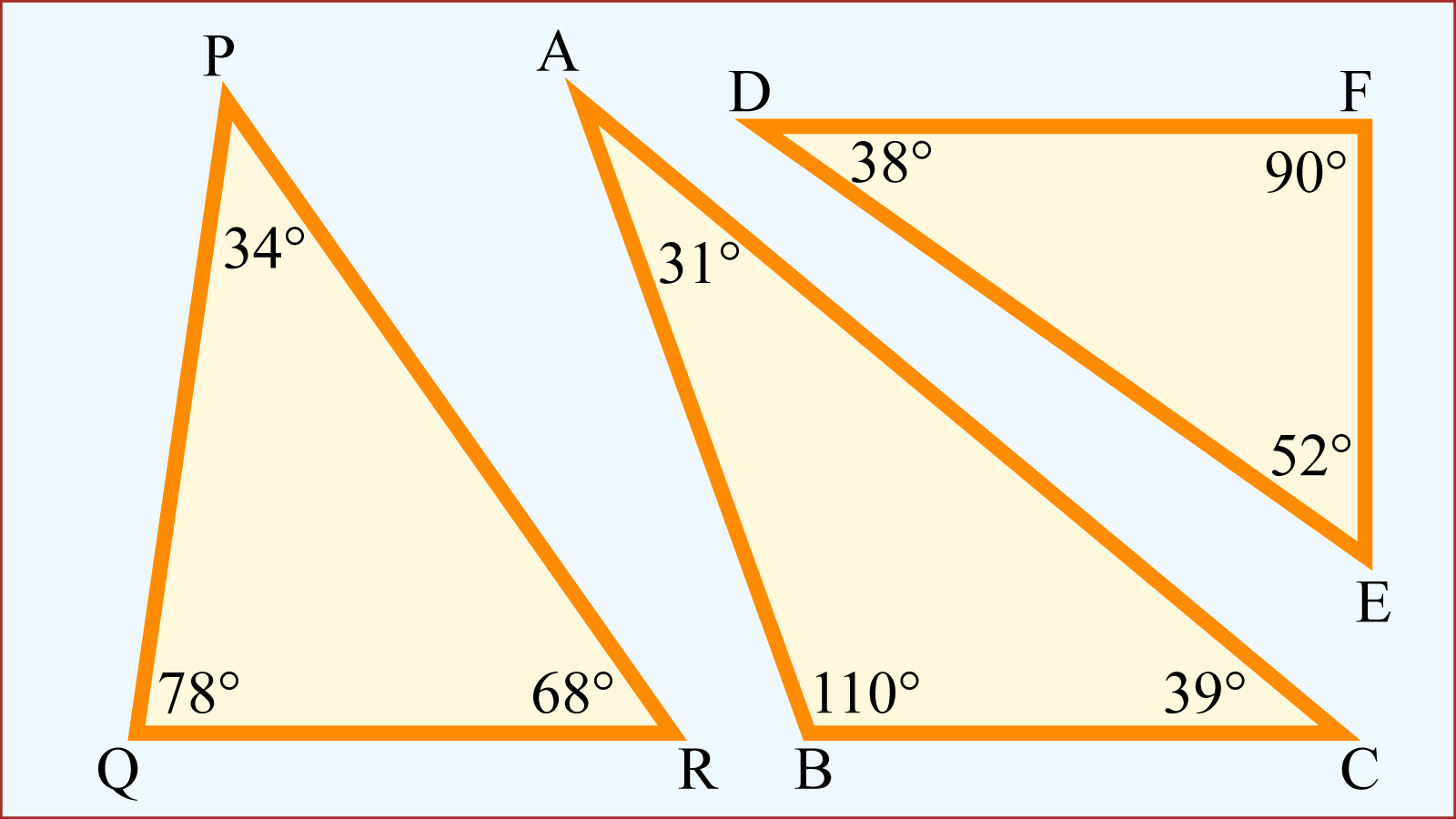
Explanation of First Triangle

In ꕔPQR, the first one in the above figure,
PQ ≠ PR, PR ≠ QR and PQ ≠ QR.
Here, the lengths of any two sides are unequal. So, this is a scalene triangle.

Again, the three angles in ꕔPQR are:
∠P = 34°, ∠Q = 78° and ∠R = 68°.
Here, all the angles are different measures and acute.

Since no two sides are equal and all angles are different and acute, hence ꕔPQR is identified as an acute scalene triangle.

Explanation of Second Triangle

In ꕔABC, the second one in the above figure,
AB ≠ AC, AC ≠ BC and AB ≠ BC.
Here, no two sides are same length. Hence, it is a scalene triangle.

Observe, the three angles in ꕔABC are:
∠A = 31°, ∠B = 110° and ∠C = 39°.
Here, all three angles are different values and one of the angles is ∠B = 110°, an obtuse angle.

In this way, one can easily identify ꕔABC as an obtuse scalene triangle.

Explanation of Third Triangle

In ꕔDEF, the third one in the above figure,
DE ≠ DF, DF ≠ EF and EF ≠ DE.
No two equal sides here. Thus, ꕔDEF is a scalene triangle.

Again, the three angles in ꕔDEF are:
∠D = 38°, ∠E = 52° and ∠F = 90°.
Here, no two angles are same; and pay attention at angle, ∠F = 90°, a right angle.

Therefore, ꕔDEF is spotted as a right scalene triangle.

Identify Scalene Triangle by Line of Symmetry

Let's dive deep to identify a scalene triangle by checking lines of symmetry for any triangle. A symmetrical line means a shape is divided into two parts by drawing an imaginary line inside the triangle such that two new shapes look like same; that is, two shapes are congruent to each other.

The figure above shows two triangles. The first one ꕔABC is an isosceles triangle whose AB = AC. Perpendicular AD is drawn to the base BC i.e., AD⊥BC. We see AD divides the ꕔABC into two triangles: ꕔABD and ꕔACD. Here, ꕔABD and ꕔACD look like same figures and ꕔABD ≅ ꕔACD. That is, ꕔABD and ꕔACD are two symmetrical shapes.

Therefore, AD is called a line of symmetry of ꕔABC.

In the second triangle ꕔPQR, on the other hand, there does not exist any line that can divide the ꕔPQR into two symmetrical shapes. More precisely, you cannot draw any line inside ꕔPQR that divides ꕔPQR into two same looking shapes.

Hence, there is no line of symmetry of ꕔABC.

Therefore, scalene triangles does not have any lines of symmetry.

If you don't find any line of symmetry of a triangle, you can reconnize the triangle as a scalene triangle.